開成中学の入試が終わりました。
算数では最小公倍数、集合を組み合わせた問題
図形と論理的思考力を交えた問題
相似形と旅人算
立体図形問題
一見難しそうに見える問題ばかりですが、実は一個一個は単純な考え方です。
例を見てみると
・1から2017までの整数のうち、3でも4でも割り切れないものを考えます。そのうち、2の倍数と5の倍数はそれぞれ何個ありますか?(大問1の2))
下のような図を書いてキの値を出せばいいと理解できればあとは単純な計算ですね!
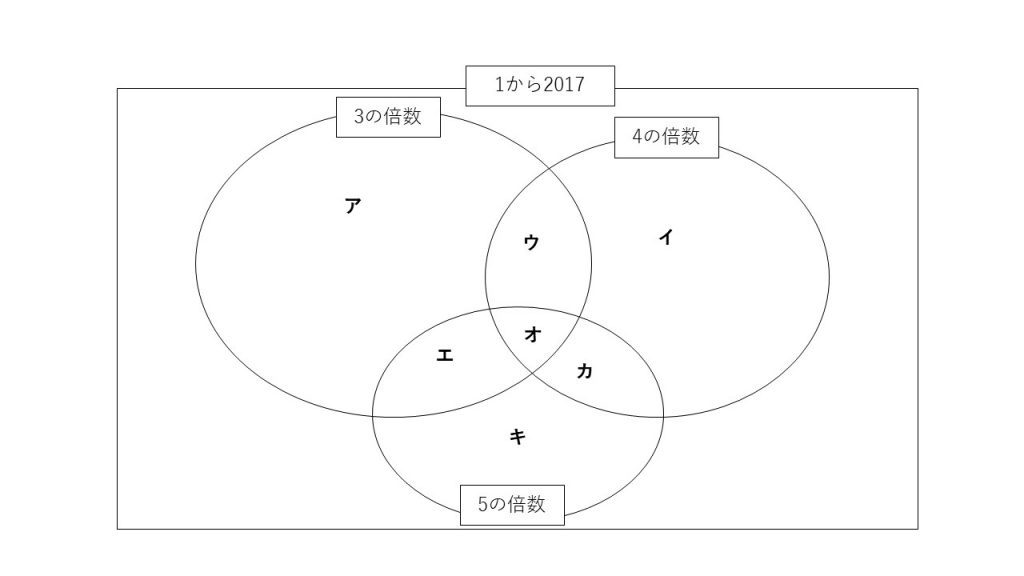
あとはただの割り算ですね。
オ=2017÷60の商=33 エ=2017÷15の商-33=101 カ=2017÷20の商-33=67 キ=2017÷5の商-エ、オ、カ=202(答)
2の倍数の場合もやり方は同様です。まぁ4の倍数を包括するというところが若干違いますが、大差はないです。
問題文をしっかり理解し論理的に解法を導く力というのはキッズビジョンが標榜する低学年時の学習で相当部分を身に着けることができます。
中学受験のみならず高校受験、大学受験、社会に出てからでも使える能力となりますので、是非キッズビジョンにお子様をお預けいただければと思います。
最後は宣伝になってしまいましたがひとまず中学受験を終えられた方お疲れさまでした。













